How to Calculate Sacco/Microfinance Loan EMI on Reducing Balance
Introduction
The reducing balance method is a formula used to charge interest on loans based on the outstanding principal.
Unlike the flat rate for loan interest calculation, the reducing balance method is cheaper especially when the loan is paid before maturity since interest for future installments is waived.
In this guide, you’ll use the reducing balance method to calculate an EMI(Equated Monthly Installment) for Sacco members.
Prerequisites
Before you begin, ensure you have the below information:
- The principal of the Loan
- The loan interest per annum usually expressed in percentage(e.g. 18% p.a)
- The repayment period(usually expressed in months). However, in some Saccos or microfinance institutions, the loan repayment period may run on a weekly or a bi-weekly basis although this is not common
Finding the EMI of a Loan in Reducing Balance
When you issue a loan to a client, you should calculate his/her EMI(Equated Monthly Installment).
Since most people seeking loans from banks or microfinance institutions earn their money on a regular basis(e.g. monthly), they need to know how much they are expected to repay in each period.
Bearing this mind, availing this information to the clients as soon as you disburse the loan to them will help them to better manage themselves financially.
The formula for finding the EMI on microfinance, banks, or Saccos is shown below:
EMI = (PRINCIPAL * (INTEREST RATE PER REPAYMENT +
(INTEREST RATE PER REPAYMENT / (((INTEREST RATE PER REPAYMENT + 1) ^ NO OF REPAYMENTS) – 1))))
Example of EMI Calculation using Reducing Balance Formula
Using the formula above, calculate the EMI of a loan using the information below:
- Principal – $100, 000/=
- Interest rate – 18% per annum
- Number of repayments – 3 months
The first step is converting the annual interest to a monthly interest by dividing it by 12. So, 18% divided by 12 equals to 1.5% or 0.05.
Now, enter the values in the formula
EMI = (PRINCIPAL * (INTEREST RATE PER REPAYMENT +
(INTEREST RATE PER REPAYMENT / (((INTEREST RATE PER REPAYMENT + 1) ^ NO OF REPAYMENTS) – 1))))
EMI = (100,000 * (0.015+
(0.015 / (((0.015+ 1) ^ 3) – 1))))
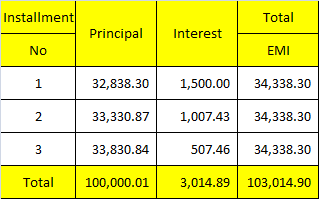
EMI = 34,338.30/=
So if you disburse a loan of $100,000/= to a client at the rate of 18% per annum repayable in 3 months, the client should pay an Equated Monthly Installment of $34,338.30/= per month
Once you determine the EMI of the loan using the reducing balance formula, the next step is to calculate the loan repayment schedule.
Calculate Interest and Principal Repayment for the 1st Month
Interest 1st month= Original Pricnipal * 0.015
Interest 1st month= $100, 000 * 0.015 = $1,500/=
Principal Payment 1st month = 34,338.30 – 1,500 = 32,838.30/=
Calculate Interest and Principal Repayment for the 2nd Month
Interest 2nd month= ($100, 000 – principal for 1st month)* 0.015
Interest 2nd month= ($100, 000 – 32,838.30)* 0.015 = $1,007.43/=
Principal Payment 2nd month = 34,338.30 – 1,007.43 = 33, 330.87/=
Calculate Interest and Principal Repayment for the 3rd Month
Interest 3rd month= ($100, 000 – principal for 1st month – principal for 2nd month)* 0.015 = $507.46/=
Interest 3rd month= ($100, 000 – 32,838.30 – 33,330.87)* 0.015 = $507.46/=
Principal Payment 3rd month = 34,338.30 – 1,007.43 = 33, 330.87/=
If you tabulate the above information, you should get the below output:
Working on the reducing balance formula manually or using a spreadsheet application is quite tiring especially if the schedule of the loan spans for more than 3 months or when working with hundreds of Sacco/Microfinance clients.
Therefore, if you want to be more productive in your bank, consider using an application like Frantek Sacco Software.
The software will keep track of all your clients and enable you to create loan accounts while it calculates the schedule in the backend within seconds even for loans with up to 100 repayments periods as shown below.
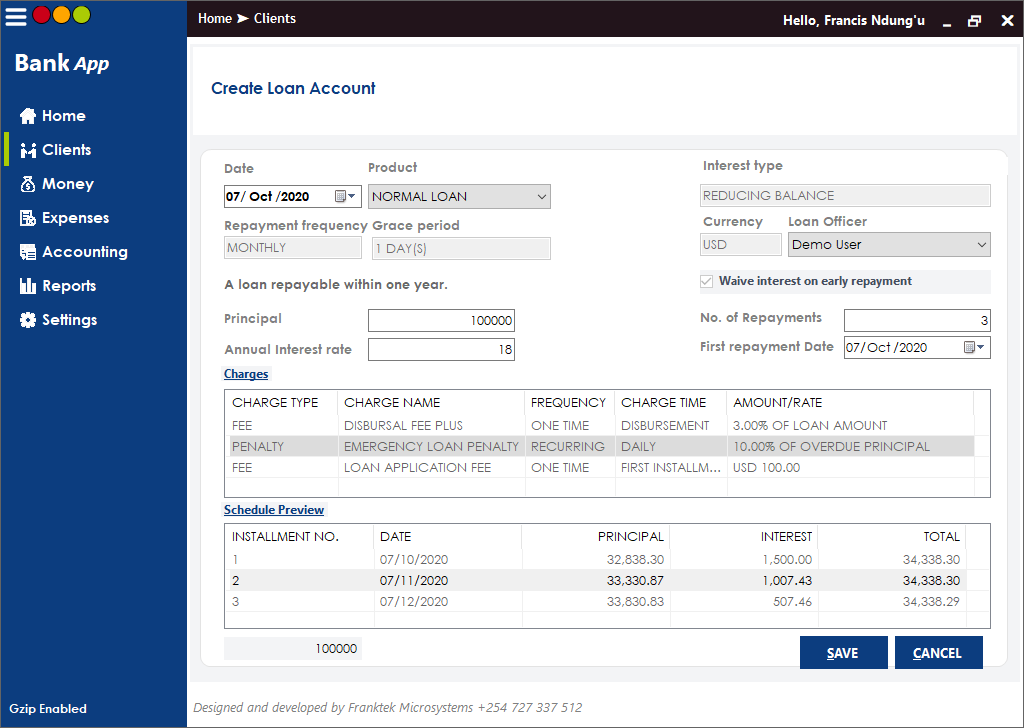
Download Franktek Sacco Software
Conclusion
In this guide, you’ve used the reducing balance formula to calculate interest for loans. Although this formula is quite complex to work with, it encourages Sacco or microfinance clients because it is cheaper than the flat rate method for loan interest calculation.

3 Comments
FRANCIS
April 10, 2021 at 2:31 pmQuite an interesting article about financial calculations. I have learnt a lot in this informative piece. Keep us posted and we shall all be financial literates.
Thank you Francis
Lawrence Maina
March 18, 2023 at 10:21 amHi,
Everything was making sense until you threw in 0.015 without explanation here it came from or how you achieved it.
Thanks
Mwandambo
March 24, 2023 at 9:10 amI was looking for reducing balance formula like the whole day then I found you… Thank you